多孔陶瓷材料的弹性模量

多孔陶瓷的用途很多，它的第二相主要是气孔，其弹性模量为零。显然多孔陶瓷材料的弹性模量要低于致密的同类陶瓷材料的弹性模量。图1给出了一些陶瓷材料的弹性模量与气孔体积分数的关系曲线。试图采用单一参量——气孔率来描述多孔陶瓷材料弹性模量的变化，但是材料的应力、应变在很大程度上取决于气孔的形态及其分布。Dean和Lopez经过仔细的研究提出一个半经验公式来计算多孔陶瓷的弹性模量E，即：

E=E₀(1-bψ_气孔)

E0为无孔状态的弹性模量；φ_气孔为气孔体积分数；

b为经验常数，主要决定于气孔的状态。

从图1可见，对于Al₂O₃和Si₃N₄实验数据与拟合曲线，有明显上凹的趋势。这可能是由于人为确定气孔形貌引起的误差。

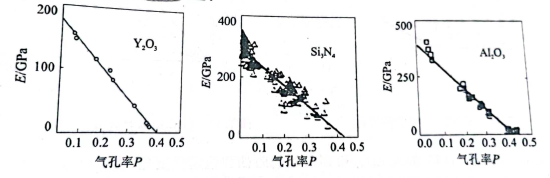
图1弹性模量E与气孔率的关系，实线为最好的拟合直线

双相陶瓷的弹性模量

弹性模量决定于原子间结合力，即键型和键能。对组织状态不敏感，因此通过热处理来改变材料的弹性模量是极为有限的。但是可以由不同组元构成二相系统的复相陶瓷，从而改变弹性模量。

总的模量可以用混合定律来描述。图2给出了两相层片相间的复相陶瓷材料的三明治结构模型图。

图2三明治结构复相陶瓷

按Voigt模型加两相应变相同，即平行层面拉伸时，则复相陶瓷的模量E_∥：

E_∥=E₁ψ₁+E₂ψ₂

按Reuss模型，假设各相的应力相同，即垂直于层面拉伸时，给出二相陶瓷材料的弹性模量E_⊥表达式：

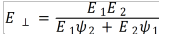
后来Hqshin和Shtrikman采取更严格的限制条件，利用复相陶瓷的有效体积模量和切变模量来计算两相陶瓷的弹性模量取得了更好的结果，在图3中列出了三种模型与实验数据的比较。该图表明混合定律是不能准确地计算复相陶瓷的弹性模量。因为等应力、等应变假设不完全合理。

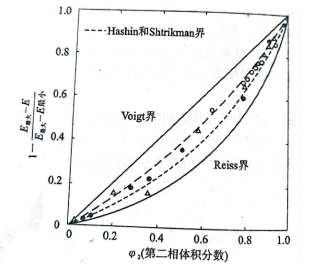
图3弹性模量计算模型和实验数据比较

图3列出了Al₂O₃加入ZrO₂和SiCw增韧时的弹性模量变化，有图可见，在其他性能允许的条件下，在一定范围内可以通过调整两相比例来获得所需的弹性模量。

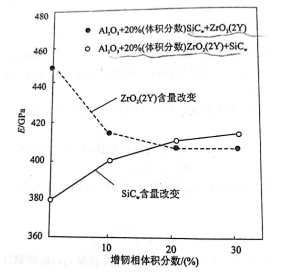
图3Al₂O₃+ZrO₂+SiC_W气相陶瓷的弹性模量